|
|
 EuroDebt NYT  EuroDebt Ch 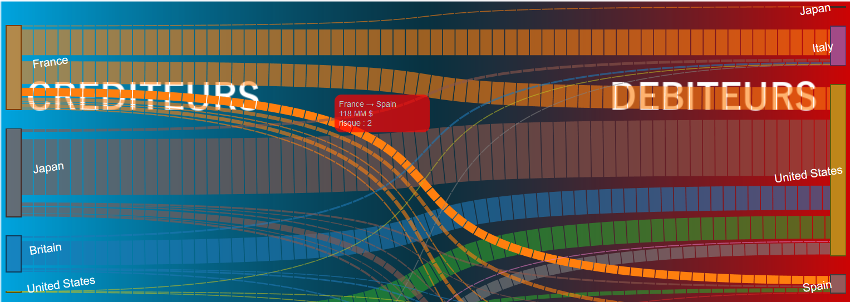 EuroDebt Sk En parcourant la belle présentation de Steve Hall sur les chord diagrams réalisés avec la librairie D3
il m’a semblé qu’un des exemples portant sur les dettes réciproques des pays européens et du G8 illustrait certaines limites des diagrammes chords.
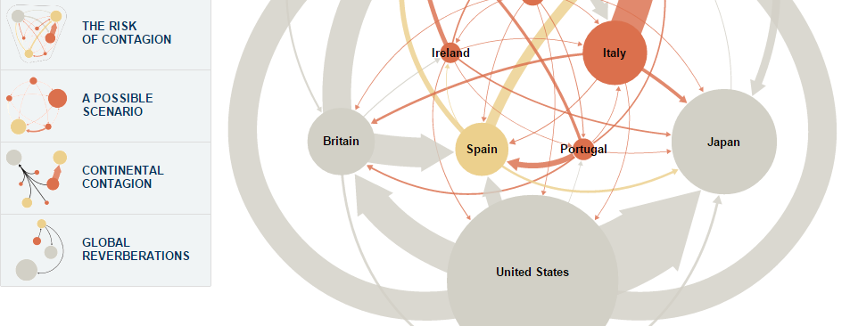
Steve Hall reprenait une datavisualisation de Bill Marsh dans le New York TimesTimes sur la crise des dettes en zone euro.
Le graphe du NYT est une séquence de graphes classiques avec des balles interconnectées et un effet pédagogique redondant: la grosse sphère des dettes américaine est soulignée par les liens massifs qui en émanent. Cet indice visuel redoublé est inhérent à ce type de graphe où largeur des liens et taille des nœuds doivent être signifiants.
Le problème avec le graphique à deux médaillons de Steve Hall est qu’il installe visuellement l’idée que dettes et créances seraient deux « entités » ou « masses » distinctes,
or c’est bien une seule réalité financière qui est vue sous deux angles, et cela pour chaque pays.
Le système des dettes est bien un circuit, ce qu’a le mérite de montrer le graphe de Bill Marsh.
Outre cela, un diagramme chord présente aussi des défauts intrinsèques.
1 – Il y a une torsion des aires et des liens qui est assez contre-intuitive pour le lecteur habitué à la convention des line graphs standards.
En effet, ces liens distendus de façon parabolique doivent représenter un état figé à un instant t , des données du type « L’Espagne doit X milliards $ à L’Angleterre » mais ces « liens aires » peuvent être très évasés à un bord et filamenteux à l’autre. Cela doit-il signifier une explosion exponentielle ou une diminution? Ce serait le cas suivant la lecture des aires sur l’axe temporel d’un graphique classique, mais ce n’est pas ce qu’illustre un diagramme chord.
2- La répartition des noms sur les 360° du cercle rend la lecture peu aisée.
3- Le chord diagram se veut plus riche en information qu’un simple graphe circulaire dont les nœuds sont homogènes en poids relatif. Mais au-delà d’un rapport de taille de 1 à 5 ou 6 les arcs de cercle qui représentent les nœuds déséquilibrent un peu trop la perception. Le lien « vers soi » qui est matérialisé par une parabole inscrite dans le cercle (voir le diagramme « Hair color »), lui non plus, n’est pas évident à déchiffrer au premier coup d’œil.
Les diagrammes Sankey en revanche, ont l’avantage de représenter une quantité donnée et ses divisions proportionnelles et ramifiées, selon l’analogie d’un fleuve et de ses affluents ou celle de la transformation d’une masse donnée en de nouvelles composantes. Un graphe Sankey présente aussi une conservation de la largeur des liens ce qui rend leur comparaison
visuelle instantanée.
L’exemple Sankey modèle de Mike Bostock présente justement un bilan énergétique du type « input / output »,
où « ce qui rentre == ce qui ressort ». Autre avantage, ce diagramme énergétique ajoute subtilement des délimitations verticales selon des catégories intermédiaires : solide/ liquide, thermique/ électrique…
En appliquant les données des dettes européennes à un graphique Sankey on aura bien la même masse monétaire vue au départ comme des créances et à l’autre opposé comme des dettes.
L’implémentation dans D3 doit être modifiée pour contourner le fait que l’algorithme définit des nœuds uniques. Contrairement à un graphe bi directionnel, un Sankey n’admet pas simultanément des liens « A vers B » et « B vers A », on va donc dédoubler les nœuds débiteurs en ajoutant par exemple une lettre « T » (pour target) puis les éliminer dans le code aux moments où il faudra retrouver le binding des data pour les éléments communs (même label, même couleur pour les nœuds…)
On trompe ainsi l’algo qui détermine deux fois plus de nœuds : les premiers seront les créanciers les seconds les débiteurs et les liens seront autorisés puisqu’ils distingueront « France as a debtor » et « France as a creditor »…
donc dans le fichier csv
creditor,debtor,amount,risk
Britain,France,22.4,3
Britain,Greece,0.55,0
France,Germany,53.8,1
France,Greece,53.9,0
devient
creditor,debtor,amount,risk
Britain,FranceT,22.4,3
Britain,GreeceT,0.55,0
France,GermanyT,53.8,1
France,GreeceT,53.9,0
Et on rétablit ensuite l’identité des nœuds pour les éléments communs ex :
.style("stroke", function(d) {
return d.color = color(d.source.name.slice(-1)=="T" ? d.source.name.substr(0,d.source.length-1) : d.source.name) ;})
Pour plus de lisibilité on place les débiteurs à gauche pour caler le mouvement « datif » de la dette sur le sens naturel de lecture de gauche à droite. On insiste en outre sur la dissymétrie en posant sur le fond un gradient coloré assez évident « bleu : tout va bien, je prête » « rouge : panique ! je dois de l’argent… » et on enfonce le clou avec une légende en transparence « créditeurs / débiteurs ».
On ajoute en info supplémentaire (avec un tooltip gradué du blanc au rouge) ce qui fait l’élément un peu choc des diagrammes de Hall et de Marsh à savoir les niveaux différenciés de risque sur certaines dettes. Alors que le NYT insiste sur l’Italie, la Grèce et Espagne placées en rouge et au centre, le graphe Sankey montre d’une part que les masses les plus importantes de dettes sont bien celles des USA et du Royaume Uni (pas la peine de les atténuer en les mettant en gris clair…) et que la fragilité de certains pays comme la France tient plus aux dettes détenues (Italie, Espagne) qu’aux dettes dues…
Autre intérêt des représentations Sankey dans D3 c’est que la disposition des liens par défaut est harmonieuse sur l’ensemble de l’espace visible mais que le graphe
est ouvert aux manipulations du lecteur qui peut réarranger des noeuds en fonction de son souhait de mettre tel ou tel effet en avant.
Exemple: si on tient à regrouper dettes et créances d’un même pays en un mini cluster.
 Sankey Euro Debts modifié. Edit : Christophe Viau (@d3visualization) signale cette version de Sankey avec « self loop »
En attendant que la version 4.6 de Unity tombe avec sa légendaire Gui, un peu de temps de à consacrer à D3 et pour les éléments de cartographie le combo
Leaflet et Mapbox. Leaflet est l’API open source sur laquelle Mapbox, service payant de cartes pour le web (webtiles) est construit.
Le premier test consiste à visualiser la fréquentation, le chiffre d’affaire et le panier moyen des enseignes paires des Champs Elysées (chiffres imaginaires).
Un bouton permet la mise à jour des séries de données, ici une pour le matin ou pour le soir. Leaflet permet de facilement animer des marqueurs et d’ajouter des formes simples
ici des cercles pour symboliser les montant en €.
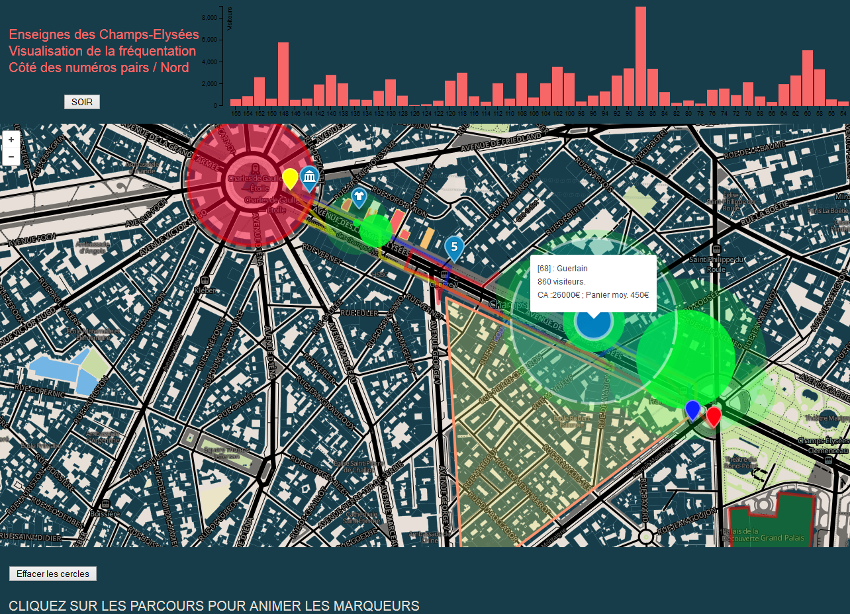 Mapbox Champs Elysées La carte éditée dans Mapbox avec les marqueurs simples non animés
 some crazy piecharts Nouvelles expérimentation à partir de la formule générale du donut typique des piecharts.
L’idée est d’associer les déformations mathématiques du traditionnel camembert à des notions plus originales.
On illustre ainsi des data par des formes rangées en portions circulaires: une statistique sur les fleurs prendra la forme d’un bouquet,
une série de chiffres sur les hélices ou les couteaux aura sa forme propre.
La formule générale pour une portion de piechart (ou de donut si on se donne aussi un rayon intérieur) est:
newVertices [6 * (i - 1)] = new Vector3 (cx - (Mathf.Abs(r - R) * Mathf.Sin (a * i)), cy, cz - (Mathf.Abs(r - R) * Mathf.Cos (a * i))); //vertex0
newVertices [6 * (i - 1) + 1] = new Vector3 (cx - (r * Mathf.Sin (a * i)), cy, cz - (r * Mathf.Cos (a * i))); //1
newVertices [6 * (i - 1) + 2] = new Vector3 (cx - (r * Mathf.Sin (a * (i + 1))), cy, cz - (r * Mathf.Cos (a * (i + 1)))); //2
newVertices [6 * (i - 1) + 3] = new Vector3 (cx - (Mathf.Abs(r - R) * Mathf.Sin (a * i)), cy, cz - (Mathf.Abs(r - R) * Mathf.Cos (a * i)));//0
newVertices [6 * (i - 1) + 4] = new Vector3 (cx - (r * Mathf.Sin (a * (i + 1))), cy, cz - (r * Mathf.Cos (a * (i + 1))));//2
newVertices [6 * (i - 1) + 5] = new Vector3 (cx - (Mathf.Abs(r - R) * Mathf.Sin (a * (i + 1))), cy, cz - (Mathf.Abs(r - R) * Mathf.Cos (a * (i + 1)))); //3
avec r et R les rayons, et {cx, cy, cz} les coordonnées du centre.L’entier i est le compteur de la boucle qui trace une portion unité par unité.
C’est en fait l’unité de base de chaque mesh crée, 6 points qui forment 2 triangles plaçés tête bêche soit un rectangle approximatif
plus ou moins déformé sur un ou plusieurs de ses côtés. Dans la forme classique il n’y a que 4 lignes différentes sur les 6 puisque 2 points (vertices) sont réutilisés.
Si on modifie nettement ces lignes identiques on donne une allure ‘dentée’ aux portions de la piechart puisqu’on révèle les 2 triangles sous jacents;
Il s’agit ensuite de tester des combinaisons de fonctions Sinus, Cosinus, Modulo, racine carrée ou valeur absolue…
// pics vers l'intérieur
newVertices [6 * (i - 1)] = new Vector3 (cx - (Mathf.Abs(r - R) * Mathf.Sin (a * i*i)), cy, cz - 1.2f*(Mathf.Abs(r - R*R) * Mathf.Cos (a * i))); // 0
newVertices [6 * (i - 1) + 1] = new Vector3 (cx - (r * Mathf.Sin (a * i)), cy, cz - (r * Mathf.Cos (a * i))); //1
newVertices [6 * (i - 1) + 2] = new Vector3 (cx - (r * Mathf.Sin (a * (i + 1))), cy, cz - (r * Mathf.Cos (a * (i + 1)))); //2
newVertices [6 * (i - 1) + 3] = new Vector3 (cx - (Mathf.Abs(r - R) * Mathf.Sin (a * i*i)), cy, cz - 1.2f*(Mathf.Abs(r - R*R) * Mathf.Cos (a * i))); //0
newVertices [6 * (i - 1) + 4] = new Vector3 (cx - (r * Mathf.Sin (a * (i + 1))), cy, cz - (r * Mathf.Cos (a * (i + 1)))); //5 2
newVertices [6 * (i - 1) + 5] = new Vector3 (cx - (Mathf.Abs(r - R) * Mathf.Sin (a * (i*i + 1))), cy, cz - 1.2f*(Mathf.Abs(r - R*R) * Mathf.Cos (a * (i + 1)))); //3
Bifurcations.fr participera à Futur en Seine en appui du Projet ‘les plus belles avenues du monde’ du cabinet INDEX3D.
L’application centrale est une maquette des Champs Elysées proposant une navigation la plus proche possible de la balade piétonne, le ’streetwalk’.
J’ai pour ma part contribué à l’élaboration de l’interface et à la
représentation des données collectables.
Venez nous rencontrer du 12 au 15 juin dans la Cour du musée des Arts et Métiers dans le secteur “ville”.
 Futur en Seine 2014
“C’est un clip musical tourné avec des figurants qui utilisent en même temps leurs téléphones portables
et postent des images sur Facebook après quoi l’équipe informe sur Twitter de l’avancée du montage…”
Lors d’une conférence de Storycode Paris sur les productions transmédia
j’ai parfois eu du mal à me représenter rapidement les liens entre les différentes plateformes, les médias et les pivots logiques
mis en oeuvre dans une production transmédia, cross médias… Si vous imaginez en plus interagir avec des capteurs temps réel,
des bases de données ou des médias classiques, un petit schéma ne peut pas faire de mal à votre grand discours…
J’ai donc eu l’idée d’une simple appli de mind mapping, Trans Média Kit,
pour représenter vite fait ces éléments par simple jeu d’icônes et de symboles.
Comme avec des cartes à jouer sur une table, on pourra y tester rapidement des idées
sous la forme d’un tableau modulaire de flux, d’éléments fonctionnels ou de contenus.
La version en cours propose de sauvegarder 6 à 8 “croquis”.
Version Android disponible sur demande à hammer.malcolm-|AT|-gmail.com
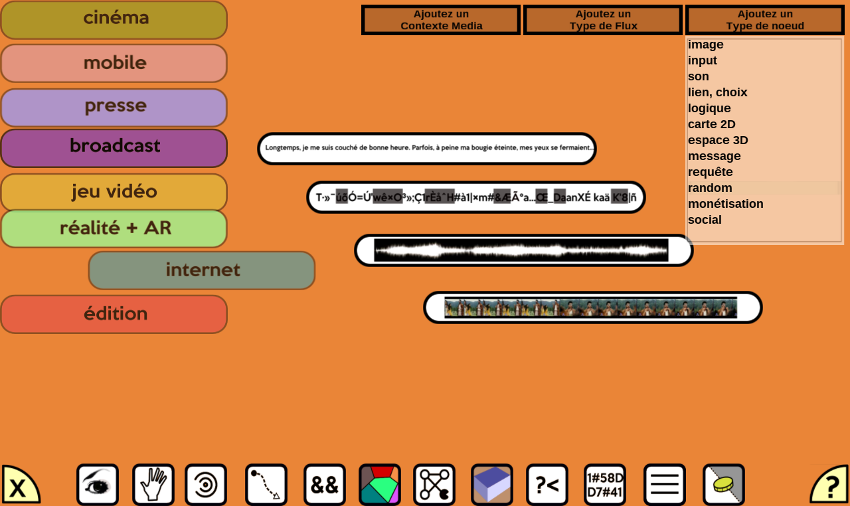 TransMedia Kit
Le chantier en cours : une application pour simplifier le travail de création des théâtreux qui ont “des idées pour l’éclairage”…
et qui ne veulent pas apprendre Unity, Blender ou autres suite logicielles dédiées à l’éclairage scénique.
Dans l’idéal parvenir à en faire une version android sinon un webplayer.
Etat actuel du projet Mise en lumières
Appliqué à distordre mes piecharts et en jouant avec le pack de shaders Colorful
je suis tombé sur des graphiques diffus, pixélisés et bavant leurs données les uns sur les autres. Rien de bien net pour les humains
sinon pour illustrer des données approximatives dans un contexte ironico futuriste. Plutôt du design pour cyborgs.
 PIES
Pour enrichir la représentation du Cac 40 (oui 40, l’incursion de la Fnac ce jour ne compte pas) l’appli comptera prochainement
un tableau des dix séances antérieures sous forme de disque bicolore. L”intérêt sera de vérifier d’un coup d’oeil la résistance d’une valeur contre un trend
ou la dispersion des valeurs. Pour l’instant l’Api Yahoo retourne parfois certaines valeurs comme manquantes (Gemalto Solvay, parfois Unibail)
d’où l’aspect échancré du disque. A éclaircir…
 archives sous forme radiale
La version Android de la visualisation du Cac 40 est livrée sur Google play.
Les pie charts d’actionnaires permettent de connaître les participations d’un actionnaire dans plusieurs sociétés de l’indice.
Ce n’est qu’une version beta destinée à trouver bugs et incompatibilités.
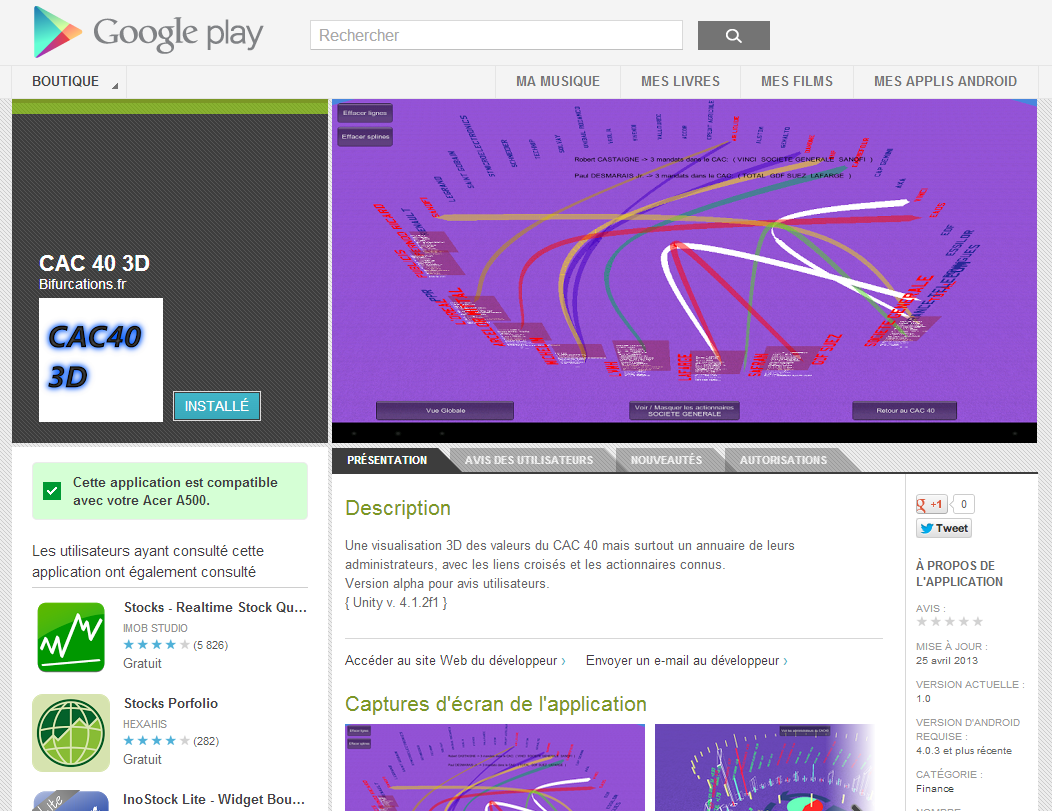 CAC 40 3D
La Loi Organique concernant la loi de Finances est un effort de simplification et de rationalisation des budgets des ministères français. Sa structure n’en demeure pas moins assez détaillée. 42loops.com, Le site de Paul Panserrieu propose une visualisation textuelle des Missions, Programmes et Actions , les trois étages de la LOLF.
A partir de la même source, le référentiel MPA, j’ai extrait une version xml de la hiérarchie de la LOLF (soit 83 Missions comprenant 211 programmes et 2956 actions) pour une première vue d’ensemble. En passant sur les cases du damier on voit les missions, puis les cylindres qui représentent les programmes et, en cliquant, le détail des actions. Les cubes générés sont proportionnels aux sommes par programmes. Les données par actions sont malheureusement perdues disponibles dans autant de fichiers PDF…
Les montants des programmes vont de quelques millions d’euros à des dizaines de milliards, les représenter avec des cubes revient à utiliser une sorte d’échelle logarithmique pour (essayer de) tout caser dans le champ de vision.
 Missions et programmes de la Loi organique sur la loi de Finances
Premiers tests pour un graphe 3d des liens entre les groupes de médias français. Navigation point & click et zoom à la molette de souris. Visionnage en Fullscreen recommandé (clic droit) .
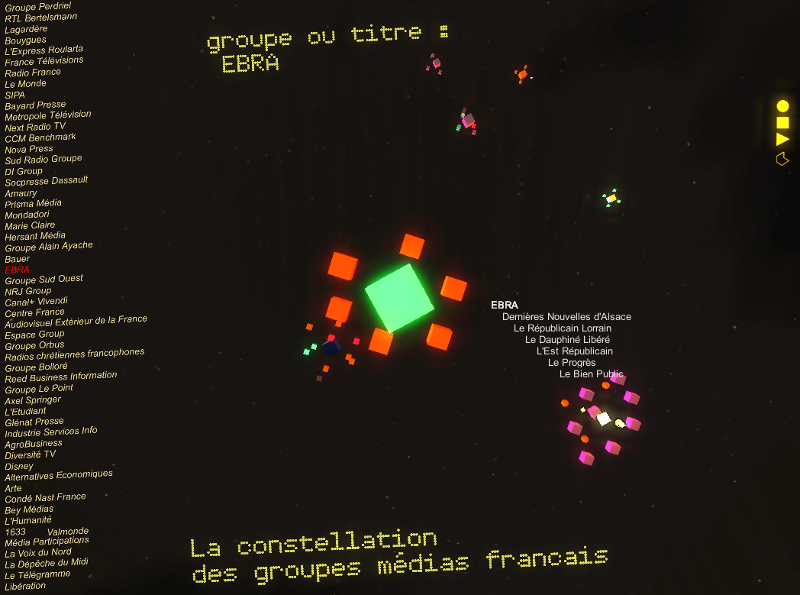 FMG
Found in the files : my first attempt to stuff a scene with gadgets: tweaked shaders, video texture, shadowed particles and split screen.
As I began studying Unity basics I was thinking to JeGX’s moto “Don’t play, code or die”.
I thought it would be nice if a coding club would teach code skills to children like the Shaolin monks.
The kind of 3D workshop JeGX promoted with his demo tool GeeXLab.
It looks like a clip for the beautiful title “Codes” by The Orb (The Dream, 2007).
 CODES
A friend of mine, Jean Marc Delaunay released a paper on the tight relationships among the board members of the 40 first companies listed in the Paris stock market the CAC40.
He gave a presentation for the Hack the press event last year in Paris.
You can see here the Flash version of the map he drew with those links.
I decided to port this 2D map to Unity 3D, adding some more info like references to the corporations to which adminitrators belong
and explicit list of memberships for each person.
Links between companies are displayed with simple straight lines or splines.
*** changes in boardmembers’ positions will be updated around as of january 2012.
Move: ZQSD + Mouse ; click a Company to browse the boardmembers, click on members for links in other boards.
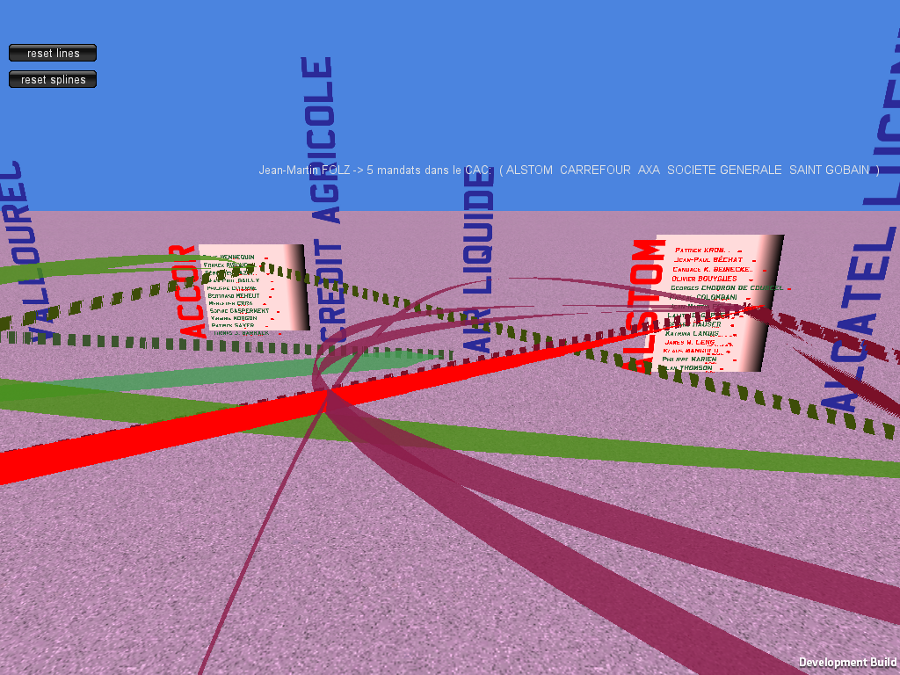 Members
fixed for 2011
- South Sudan split from North
- Somaliland is displayed as an autonomous country
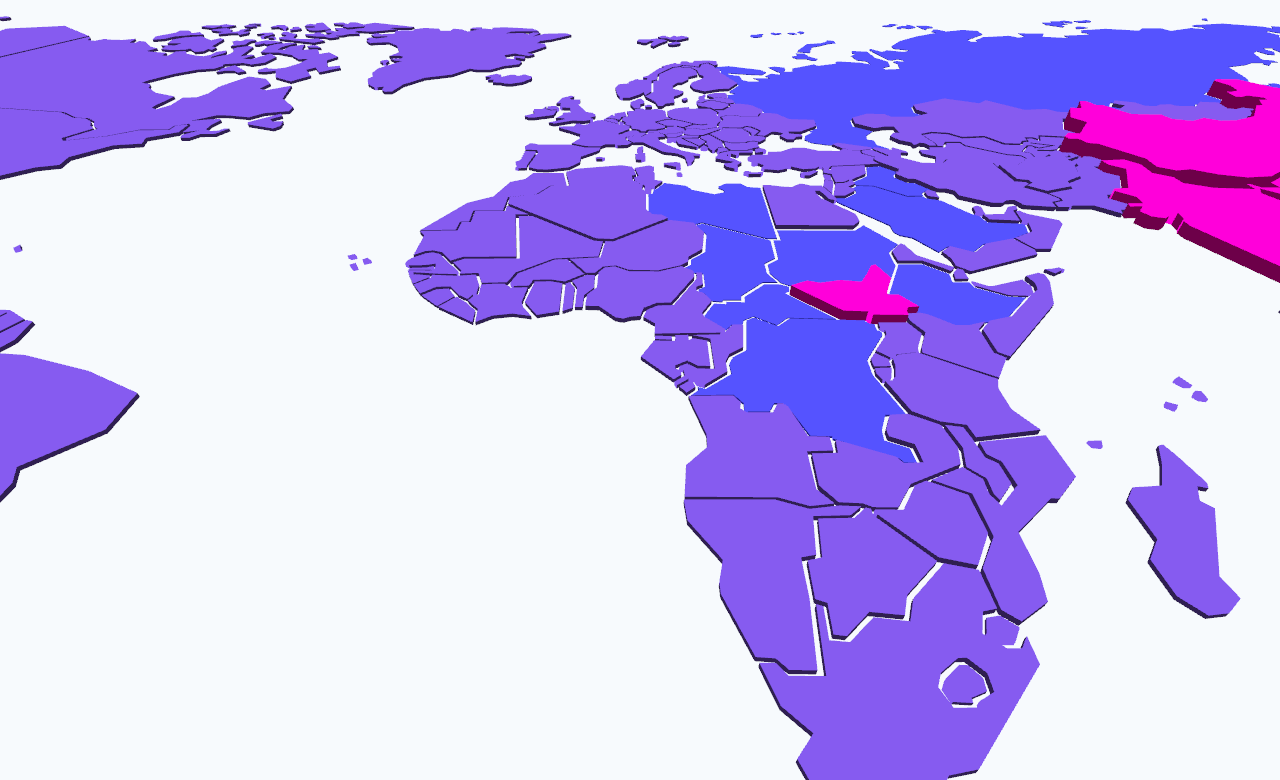 171 meshplanes 171 extrudes meshes 1 global meshplane
The Silicon Maniacs event Silicon Radio held in La Cantine, Paris
called for audio creations to be streamed within their 13 hours radio show.
The Theme was “How do you (fore)see the future ?”
I envisioned the year 2070 where Skype will be a time machine and Google have plans to change the alphabets…
Audio is fine, so I submitted an audio file but
3D nowadays is the Baal machine thats swallows any media don’t you think ?
So I send Unity web and Android version too.
The Unity pro version allows some sound variations with reverb zones,
the Android basic is useful as a downsizing exercice.
> Here for Unity live Demo
> Here for the android version

I was looking for blank maps to use within Unity. But did not find anything useful since each country needs its own mesh. I took the standards : SVG map from Wikipedia, a path conversion script from Blender. Some corrupted vertices had to be fixed by hand. 170 from the 192 UNO states are figured as meshplanes and fully scriptable.
The Android version is tested on Acer Iconia A500 (multitouch of 10).
The extrusion transitions are powered by iTween library.
Move with Z Q S D and Mousewheel. Right click for Full screen view.
World map démo here

 Try the Android version (2.3+) Try the Android version (2.3+)
|
|


















 Try the Android version (2.3+)
Try the Android version (2.3+)